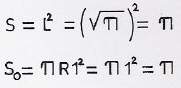Cuadratura del círculo
| ||||||
Cuadratura del círculo: tratar de calcular la superficie de un círculo sacando el promedio de las áreas de dos polígonos regulares, uno inscrito y otro circunscrito. Es uno de los tres problemas de la Grecia clásica, los otros dos son la duplicación del cubo y la trisección del ángulo, que los matemáticos griegos intentaron resolver utilizando únicamente la regla y el compás. Este famoso enigma, tuvo una repercusión tal que mantuvo en vilo a varias generaciones de matemáticos, contribuyendo notablemente al desarrollo de la matemática del Período helénico. Éste intento continuó, por matemáticos de todo el mundo hasta finales del siglo XIX.
Efectivamente, fue el matemático alemán Ferdinand Lindemann, quien en 1882 demostró que el número π era trascendente y por tanto el problema irresoluble.
Historia
El primer matemático que intentó resolver este problema fue Anaxágoras de Clezomone (499 - 428). Hipócrates de Chios (470 a.n.e) también dedicó grandes esfuerzos pero sin éxito.
Otros matemáticos griegos, no vinculados a la Escuela de Platón buscaron respuestas al problema obviando la restricción del uso exclusivo de la regla y el compás, tal es el caso de Dinóstrato (siglo IV a.n.e), el cual utilizando la Cuadratriz de Hipias demuestra que es posible rectificar la circunferencia y, por consiguiente, es posible resolver la cuadratura del círculo, aunque sin la restricción del solo uso de la regla y el compás.
A la solución de este problema también contribuyeron Antifón (siglo V a.n.e) y Brisón (siglo IV a.n.e), la solución aproximada de Antifón sugirió a Arquímedes de Siracusa (187–212) su importante descubrimiento, la determinación de la medida de la circunferencia y del área del círculo a partir de π.
Arquímides, con la diáfana visión que lo caracteriza, desecha la posibilidad de construir la solución con regla y compás y se fundamenta en que la longitud de la circunferencia está comprendida entre las longitudes de los polígonos regulares inscritos y circunscritos. En este procedimiento se marca el inicio del método que hoy se llama paso al límite.
Descripción del problema
El problema consiste en la búsqueda de un cuadrado de área equivalente a la de un círculo dado. El problema se enuncia de la siguiente forma: Determinar, utilizando solamente la regla y el compás, el lado de un cuadrado de área equivalente al área de un círculo de radio dado.
Una construcción geométrica aproximada de la cuadratura del círculo con regla y compás con tales fines "pedagógicos" o simplemente recreativos debería cumplir los siguientes requisitos:
- la aproximación de pi debería ser la mejor posible
- el número de pasos debería ser el mínimo posible
- la construcción debería poder hacerse siguiendo la lógica de cualquier problema: partir del dato ... para llegar a la solución, en este caso partir del radio del círculo (el dato) para llegar al lado del cuadrado (la solución).
Solución del problema
La solución del problema de la Cuadratura del Círculo conduce a la ecuación que tiene como variable la medida del lado del cuadrado de área equivalente al área del círculo de radio unidad. Esta ecuación es x2= π, en ella el coeficiente π del término independiente no es algebraico, en 1882 Ferdinand Lindermann (1852 – 1939) demostró que π es trascendente y no algebraico, por tanto, no podía ser raíz de una ecuación algebraica con coeficientes racionales. Con este resultado quedaba definitivamente probado que no puede cuadrarse un círculo de radio dado.
El enfoque aproximado que se le dio a este problema en la Grecia Antigua condujo a la introducción de aproximaciones del área del círculo por polígonos inscritos o circunscritos y al cálculo aproximado del número π. La enorme cantidad de esfuerzos por cuadrar exactamente el círculo no pudo conducir al éxito y de ahí la naturaleza trascendente de este problema.
A pesar de esto, se ha seguido buscando métodos geométricos de aproximación hasta nuestros días, incluso por matemáticos prestigiosos. Se busca una construcción sencilla, elegante y con el menor número de pasos.
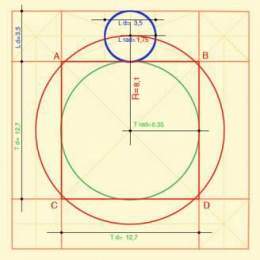
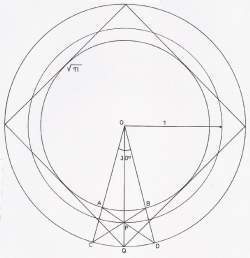
Dado un círculo , C1, de radio R1=1, un cuadrado inscrito en él, de lado 
y otro círculo, C2 inscrito en dicho cuadrado y de radio 
vamos a demostrar que existe un circulo, C3, entre C1 y C2, cuya superficie es igual a la del cuadrado dado y cuyo radio, R3, vamos a determinar.
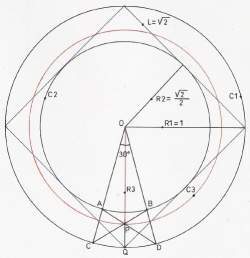
a) Desde el centro, O, trazamos un ángulo de 30º que determina los puntos de corte A, B, C, D, con los círculos C2 y C1 respectivamente y teniendo al radio OQ como bisectriz. b) Trazamos los segmentos AD y BC, y donde se cortan determina el punto P sobre el radio OQ. El Segmento OP, es el radio R3 del circulo C3, buscado.
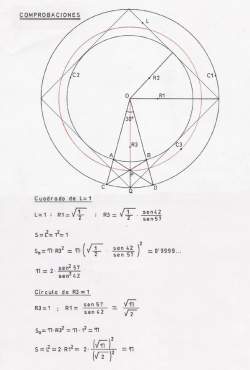
Determinación del segmento OP = R3 Aplicando el teorema de los senos para la resolución de triángulos oblicuángulos y considerando que sen 123º = sen 57º por ser ángulos complementarios y OD = 1
De la hipótesis inicial tenemos: superficie del cuadrado de lado igual superficie del círculo de radio R3.
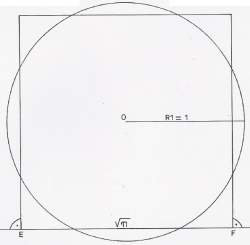
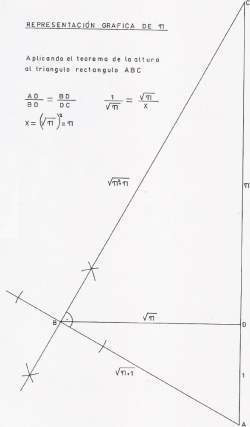
Representamos esta igualdad geométricamente, aplicando el teorema de proporcionalidad en el triángulo rectángulo NEF:
Con el segmento 
obtenido, y trazando perpendiculares en E y F, construimos un cuadrado, y desde su centro, un círculo de radio R1 = 1
Es la cuadratura del círculo con regla y compás.
Demostración de la determinación geométrica del punto P y que cumple: OP = 1 para 
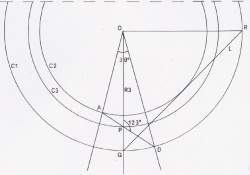
Dado un círculo, C3, de radio R3, hallar el lado, L, de un cuadrado cuya superficie sea igual a la del círculo dado.
Trazamos un ángulo de 30º, con vértice en O, teniendo a R3 como bisectriz; y el punto de corte P.
Con vértice en P, trazamos un ángulo de 123º, determinando los puntos de corte A y D que nos dan los radios OA y OD de las circunferencias C2 y C1 respectivamente.
- Proyectando OP hasta su corte con C1 nos da el punto Q que uniéndolo con el punto R nos da el lado, L. buscado.
Fuentes
- Davinson, J. y otros.(1995). Problemas de matemática elemental 2. La Habana: Pueblo y Educación.
- Ribnikov. K.(1991). Historia de las Matemáticas. Moscú: MIR.
- Por qué debemos enterrar las matemáticas escolares
- LA CUADRATURA DEL CIRCULO: UN PROBLEMA INSOLUBLE PERO DIVERTIDO.
- Secrets Of The Great Pyramid
