Distancia euclídea
| ||||||
Distancia euclidea. En matemáticas, álgebra, geometría y, más específicamente, en análisis real, análisis complejo y geometría analítica, se trata de una función no negativa usada en diversos contextos para calcular la distancia entre dos puntos , primero en el plano y luego en el espacio. También sirve para definir la distancia entre dos puntos en otros tipos de espacios de tres o más dimensiones. Y para hallar la longitud de un segmento definido por dos puntos de una recta, del plano o de espacios de mayor dimensión.
Base
Sus bases se encuentran en la aplicación del Teorema de Pitágoras sobre triángulos rectángulos, donde la distancia euclideana viene a ser por lo general la longitud de la hipotenusa del triángulo recto conformado por cada punto y los vectores proyectados sobre los ejes directores al nivel de la hipotenusa.
Definiciones
En el plano cartesiano sean los puntos A=(xA;yA) B=(xB;yB) se define la distancia euclideana entre dichos puntos por:
En el espacio, sean los puntos A=(xA;yA;zA) y B=(xB;yB;zB) se define la distancia euclideana mediante la expresión:
Y de manera más general en un espacio de N dimensiones la distancia euclideana entre dos puntos A=(a1;a2;...;aN) y B=(b1;b2;...;bN) se ajusta a:
De manera general la métrica euclideana entre dos puntos se define como: la longitud del segmento de recta que une a dichos puntos.
Propiedades
La distancia o métrica euclideana (en su caso general de N dimensiones) satisface las condiciones necesarias para ser catalogada como una métrica en términos estrictamente matemáticos que serían:
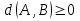
- d(A,B)=d(B,A). Llamada propiedad simétrica [1]
- d(A,A)=0.
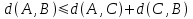. Llamada propiedad de la desigualdad triangular. [2]- Si d(A,B)=0, entonces A=B.
Las pruebas son triviales.
Importancia
Además del evidente resultado de la determinación de la longitud de un segmento de recta o la distancia entre dos puntos, pueden citarse otras muchas aplicaciones de la distancia euclideana, que dicho sea de paso, se conoce como distancia a secas.
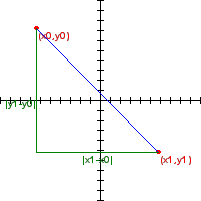
Tiene sus bases en el teorema de Pitágoras donde como se ve en la figura siguiente:
donde la distancia misma es la longitud de la hipotenusa (marcada en azul en la figura) y sus catetos (trazados en verde), que serían las proyecciones sobre los ejes coordenados de dicha recta, trasladados hasta los puntos en cuestión (marcados en rojo). Acá el conocido teorema se expresa:
- |AB|2=(xB-xA)2+(yB-yA)2'
que luego queda en la conocida fórmula de la distancia euclideana.
Un caso menos conocido es su uso en el espacio tridimensional de colores RGB cuyas dimensiones suelen definirse como valores enteros no negativos que varían desde 0 hasta 255 (lo que soporta un octeto o byte) y que permite contar con 2563=16.777.216 colores, mucho más de lo que el ojo humano puede distinguir. En este espacio cada punto indica un color distinto dado por el brillo de cada componente: 0 es oscuro total; 255, brillo máximos de la componente. Por ejemplo: (255,0,0) es rojo brillante, (127,0,0) es un rojo más oscuro, (64,0,0) es rojo más oscuro aún, (0,0,0) es negro. Activando el resto de las componentes se logran otras combinaciones de color.
En este caso la distancia euclideana se define para dos puntos A=(rA;gA;bA) y B=(rB;gB;bB) del espacio de color RGB:
que permite entre otras muchas cosas la detección automatizada de bordes y por tanto, de objetos completos en fotografía digital y por ende, en la edición digital de video.
Inconvenientes
La métrica euclidiana pese a ser la más simple de las distancias a determinar y calcular por su relación con otros resultados bien conocidos de las matemáticas; presenta evidentes inconvenientes de aplicación fuera de espacios donde la línea recta sea la menor distancia que conecta a dos puntos.
Un ejemplo más que evidente es nuestra propia Tierra. La forma esférica de la misma y la incapacidad de viajar en línea recta porque habría que hacerlo por debajo del suelo, impiden el uso de este tipo de distancia sobre el planeta. Para ello existen otras métricas como la esférica e incluso, otras más abstractas para casos más complejos.
En el particular de una esfera, la distancia más corta entre dos puntos es el arco que los une.
Referencias
Fuentes.
- Bronshtein I., Semendiaev K. Manual de matemáticas para ingenieros y estudiantes. 2da Edición. Moscú, Editorial Mir, 1973.
- Colectivo de autores. Matemática 11no grado. La Habana,Editorial Pueblo y Educación, 1989.
- Artículo: Teorema de los senos. Disponible en: "es.wikipedia.org". Consultado: 17 de junio de 2012.
