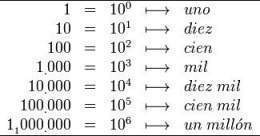Diferencia entre revisiones de «Sistema de numeración»
(→Representación de Números Negativos) |
|||
| Línea 385: | Línea 385: | ||
A6 A5 A4 A3 A2 A1 A0 | A6 A5 A4 A3 A2 A1 A0 | ||
0 1 1 0 1 0 0 | 0 1 1 0 1 0 0 | ||
| − | + | 0 110100 | |
(+) Magnitud del numero | (+) Magnitud del numero | ||
| Línea 439: | Línea 439: | ||
Un número positivo en cualquier representación tiene un cero en el bit de la extrema izquierda para un (+), seguido de un número positivo. Un número negativo siempre tiene un uno en el bit de la extrema izquierda para un (-),pero los bits de magnitud se representan de una forma diferente. | Un número positivo en cualquier representación tiene un cero en el bit de la extrema izquierda para un (+), seguido de un número positivo. Un número negativo siempre tiene un uno en el bit de la extrema izquierda para un (-),pero los bits de magnitud se representan de una forma diferente. | ||
| − | En la representación de signo-magnitud, estos bits son el número positivo ; en la representación de complemento de 1, estos bits son el complemento del número binario y en la representación de complemento 2, el número esta en su forma de complemento 2. | + | En la representación de signo-magnitud, estos bits son el número positivo ; en la representación de complemento de 1, estos bits son el complemento del número binario y en la representación de complemento 2, el número esta en su forma de complemento 2. |
==Fuentes== | ==Fuentes== | ||
Revisión del 15:31 8 mar 2012
| ||||||
Sistema Numérico. Conjunto de reglas y convenios que permiten la representación de todos los números, a partir de un grupo limitado de símbolos.
Sumario
Tipos
- Posicional: Es aquel en que el valor de la cifra cambia según la posición que ocupa la cifra dentro del número. Ej.: sistemas binario, decimal, Hexadecimal, octal, etc.
- No posicional: Es aquel en el que el valor de la cifra no depende de la posición que ocupe dentro del número .Lo que indica que existen dos tipos de valores de las cifras Ej.:Los números romanos.
Base
Es igual a la cantidad de dígitos diferentes que posee el sistema, a partir de los cuales se puede representar cualquier número.
Ejemplos:
- Sistema Decimal: 10 dígitos: (0,1,2,3,4,5,6,7,8,9)
- Sistema Binario: 2 dígitos: (0,1)
Sistemas Numéricos Posicionales
En el sistema de números decimales se dice que la base o raíz es 10 debido a que usa 10 dígitos, y los coeficientes se multiplican por potencias de 10.
El sistema binario únicamente posee dos valores posibles que son 0 y 1, en los cuales cada coeficiente AJ se multiplica por 2J, como ejemplo tendremos el desarrollo del número binario 11010.11 el cual será representado por la siguiente manera :
1*24+1*23+0*22+1*21+0*20+1*2-1+1*2-2 16+8+0+2+0+0.5+0.25 = 26.75
Por lo tanto tenemos que un número en un sistema de base(r) tiene coeficientes multiplicados por potencias de (r) y quedaría representado de la siguiente manera : an*rn+ an*rn+ . . . + a2*r2+ a1*r1+ a0*r0+ a-1*r-1+ . . . + a-m*r-m
Sistema Binario
En el sistema binario la base es 2 y sólo se requieren dos cifras, el 0 y el 1 por consiguiente para representar un número. Las cifras 0 y 1 tienen el mismo significado que en el sistema decimal, pero difieren en cuanto a la posición que ocupan. En el sistema binario el dígito individual representa el coeficiente de las potencias de dos (2) en lugar de las de diez (10), como sucede en el sistema decimal. El valor de cualquier número expresado en el sistema numérico binario es igual a la suma de los términos que resulten de multiplicar cada uno de los dígitos que constituyen el número en cuestión por las potencias de 2 que corresponda según la posición que ocupe dicho dígito dentro del número.
Ejemplo: El número decimal 19 se escribe en representación binaria como 10011 ya que:
- 10011=1x24 + 0x23 + 0x22+1x21+1x20
- 10011= 16 + 0 + 0 + 2+ 1 =19
Sistema Decimal
Es el sistema utilizado habitualmente, base 10 y tiene diez dígitos, del 0 al 9. El valor de cualquier número expresado en este sistema es igual a la suma de los términos que resulten de multiplicar cada uno de los dígitos que constituyen el número en cuestión por la potencia de 10 que corresponda según la posición que ocupe dicho dígito dentro del número. Para escribir un número mayor que 9, asignaremos un significado a la posición de cada cifra en el número completo.
Ejemplo: El número 1264
- 1264= 1x103+ 2x102+ 6x101+ 4x100
Sistema Octal
De la misma manera que el sistema decimal, el sistema octal necesita ocho cifras para poder expresar o representar cualquier número. La base de éste sistema es 8 .Está formado por los dígitos 0,1,2,3,4,5,6,7.
Sistema Hexadecimal
Este sistema necesita 16 cifras como base para expresar o representar cualquier número, los primeros diez dígitos de este sistema coinciden con los del sistema numérico decimal y los restantes seis dígitos se toman como las seis primeras letras (mayúsculas) del alfabeto: A,B,C,D,E,F, o sea: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, F; por primera vez aparecerán combinaciones de dígitos, uno de los cuales puede ser una letra pero que para los efectos del sistema Hexadecimal es considerado un número. Al igual que en los dos casos anteriores, el valor de cualquier número expresado en el sistema numérico hexadecimal es igual a la suma de los términos que resulten de multiplicar cada uno de los dígitos que constituyen el número en cuestión por la potencia de 16 que corresponda según la posición que ocupe dicho dígito dentro del número.
Ejemplo 1-1: Para comprender mejor todo lo anterior vamos a ilustrar lo dicho con un número expresado en cada uno de los tres sistemas numéricos mencionados. Tomemos el número 154, escrito en el sistema numérico decimal.
154 = 1(10*2) + 5(10*1) + 4(10*0) = 1(100) + 5(10) + 4(1) = 100 + 50 + 4 = 154
Este mismo número en el sistema binario se representa por la cadena de 8 bits 10011010 10011010 = 1(2*7) + 0(2*6) + 0(2*5) + 1(2*4) + 1(2*3) + 0(2*2) + 1(2*1) + 0(2*0) = 1(128) + 0(64) + 0(32) + 1(16) + 1(8) + 0(4) + 1(2) + 0(1) = 128 + 0 + 0 + 16 + 8 + 0 + 2 + 0 = 154
En el sistema numérico hexadecimal se escribe como 9A 9A = 9(16*1) + A(16 *0) = 9(16) + 10(1) = 144 + 10 = 154
Por lo tanto, 154 = 10011010b = 9Ah (La b y la h significan que el número está expresado en el sistema binario y en el hexadecimal, respectivamente). Como se ve, la cadena de dígitos necesario para representar un número aumenta al disminuir la base del sistema. La ventaja del sistema binario consiste en que el valor de sus dígitos (llamados frecuentemente bits) coincide con los valores de 1 y 0 que se utilizan en la Electrónica Digital para caracterizar los niveles alto y bajo de las señales con que operan normalmente los circuitos lógicos. Su inconveniente, además de no ser tan familiar como el sistema decimal, es que los números requieren cadenas muy largas para representarlos. Para resolver esta última desventaja y a la vez conservar su ventaja, se puede utilizar un sistema numérico cuya base sea mayor que 2 pero que sea una potencia de ese número. La base que resulta más conveniente es 2*4, o sea 16, que es precisamente la base del sistema numérico hexadecimal.
Conversión de números
Este método consiste en dividir reiteradas veces un número entre la base del sistema que se desea, hasta encontrar un cociente tal que no sea divisible por el divisor o la base. Después se toma éste último cociente y los restos, de derecha a izquierda, formándose así el número en el sistema solicitado.
Decimal-Binario
Un número binario (x) puede convertirse en decimal efectuando la suma de las potencias cuyo valor es uno.
Ejemplo : (1010.011)2 = 1*2³+0*2²+1*2¹+0*2º+0*2־¹+1*2־²+1*2־³
= 8+0+2+0+0+0.25+0.125 = 10.375
Para los números expresados en base (r) podríamos efectuar su conversión a decimal multiplicando cada coeficiente por la potencia correspondiente de r y sumando.
Ejemplo : (630.4)8 = 6*82+3*81+0*80+4*8-1
= 384+24+0.5 = 408.5
Cuando deseamos efectuar la conversión de decimal a binario o a cualquier otro sistema con base r es mas conveniente si el número se separa en parte entera y en una parte fraccionaria, y la conversión de cada parte se efectúa por separado :
Ejemplo : Convertir el número (41)10 a binario
41 1 LSB
20 0
10 0
5 1
2 0
1 1 MSB
(41)10 = (101001)2
Para convertir cualquier entero decimal en cualquier sistema de base r la división se hace entre r en lugar de 2.
Ejemplo : Convertir el número (153)10 a base 8
153 1 LSB 198 3
2 2 MSB
(153)10=(231)8
Para convertir una fracción decimal a binario, el sistema que se sigue es similar al que utilizamos para los enteros, sin embargo, se usa la multiplicación en lugar de la división, y los enteros se acumulan en lugar de los residuos.
Ejemplo : convertir (0.6875)10 a base 2
Entero Fracción Coeficiente 0.6875 *2 1 0.3750 a-1 = 1 0.3750 *2 0 0.75 a-2 = 0 0.75 *2 1 0.5 a-3 = 1 0.5 *2 1 0.0 a-4 = 1 (0.6875)10=(0.1011)2
Cuando deseamos convertir una fracción decimal en número expresado en base r, el procedimiento es similar, la multiplicación se hace con r en lugar de 2 y los coeficientes se encuentran con los enteros.
Ejemplo : convertir (0.513)10 a base 8
Entero Fracción Coeficiente
0.513 *840.104 a-1 = 4
0.104 *800.832 a-2 = 0
0.832 *860.656 a-3 = 6
0.656 *850.248 a-4 = 5
0.248 *810.984 a-5 = 1
0.984 *870.872 a-6 = 7
Cuando deseamos hacer la conversión de un número decimal de una parte entera y una parte fraccionaria la conversión se hace por separado y posteriormente se combinan las dos respuestas.
Ejemplo : (41.6875)10 -> (101001.1011)2
Ejemplo: Necesitamos convertir el número 14 en binario.
Para ello dividimos el número 14 por 2, que es la base del sistema en el que lo queremos representar, tantas veces como sea posible hasta llegar a un resto que no se pueda dividir más. En cada división, si no hay resto se coloca “0” y si queda algún resto se coloca “1”. Si este proceso se realiza manual es mucho más fácil identificar el número binario resultante. La base del sistema al cual se hizo la conversión se coloca en el extremo inferior derecho. De modo que tomamos de derecha a izquierda el último cociente y los otros restos. Vea como sigue: 14/2=7 7/2=3 3÷2=1— (0 1 1 — restos y el último cociente es 1.).
De modo que el número 14 en decimal se representa 11102 en binario.
Decimal-Octal
Para ello realizamos una operación parecida a la conversión anterior. Procedemos a dividir el número en cuestión por la base del sistema a convertir.
Ejemplo: tenemos el número 243.
Al dividirlo por 8 que es la base del sistema octal, resulta ser 30, con un primer resto de 3, al proceder a dividir 30 entre 8, resulta ser 24, por lo que el resto es 6 y el último cociente es 3. Tomando de derecha a izquierda queda 363. De modo que el 243 en el sistema decimal es 3638 en el sistema octal 243/8=30 30/8=3 (3 6 restos) 3 — ultimo cociente.
Decimal-Hexadecimal
Ejemplo: Tenemos el número 243 y deseamos convertirlo en hexadecimal. Procedemos de manera similar a las conversiones anteriores.
Dividimos el número 243 por la base 16. Al hacerlo obtenemos un cociente de 15 con un resto de 3, de modo que tomamos de derecha a izquierda:último cociente(15) y el resto que es 3. En hexadecimal el 15 se representa por la letra F, completándose el resultado. El número 243 en decimal corresponde al F316 en hexadecimal.
Números octales y hexadecimales
Las conversiones entre código binario, octal y hexadecimal es muy importante en las comparaciones digitales, ya que cada dígito octal corresponde a tres dígitos binarios y a cada dígito hexadecimal corresponde cuatro dígitos binarios. (10110001101011.111100000110)2 -> (26153.7406)8
Cuando deseamos convertir un número binario a hexadecimal, el proceso es similar excepto que el número binario se divide en grupos de 4. (10110001101011.11110010)2 -> (2C6B.F2)16
La conversión a hexadecimal en binario se realiza con un procedimiento inverso al anterior esto es; cada dígito octal se convierte en su equivalente binario de tres dígitos y cada dígito hexadecimal se convierte en su equivalente binario de cuatro dígitos.
Conversión al sistema decimal
Para ello se utiliza el método de multiplicación de potencias sucesivas.
De binario a decimal
Convertir el número 111100112 a decimal. El número binario contiene ocho dígitos, por lo que debemos realizar una suma de cada dígito multiplicado por 2 elevado a la potencia correspondiente comenzando por 0, 1, 2 ….n, hasta el último digito.
Esta operación la realizamos de derecha a izquierda.
En este caso sería: 1x20+ 1x21+ 0x22+ 0x23+ 1x24+1x25+ 1x26+ 1x27=1+2+0+0+16+32+64+128=243 De modo que el número 111100112 es igual a 243 en el sistema decimal.
De octal a decimal
Se realiza demanera similar a la anterior pero teniendo en cuenta que la base del sistema ahora es ocho (8).
322258= 5x80+ 2x81+ 2x82+ 2x83+ 3x84= 5+16+128+1024+12288 =5+16+128+1024+12288=13461
De hexadecimal a decimal
Esta operación la realizamos de derecha a izquierda. Tomamos cada dígito, lo multiplicamos por la base 8 elevada primero a 0, a uno, ect. Debemos recordar que el valor de F en el sistema decimal es 15. Comenzamos: FF16= Fx160+Fx161=15x160+15x161=15x1+15x16=15+240=255 De modo que el número FF de base 16 es equivalente al 255 de base 10.
Operaciones en Sistemas Numéricos
Complementos Este tipo de operación se utilizan en las computadoras digitales para simplificar la operación de sustracción y para manipulaciones lógicas.
Existen 2 tipos de complementos:
a) El complemento de r.
El complemento de r de un número positivo N en base r con una parte entera de n dígitos, será definido como el complemento de r a n y se define como rn-N;
Obtener el complemento de 10 de (52520)10
105-52520=47480
Obtener el complemento de 10 de (0.3267)10 100-0.3267=0.6733
Obtener el complemento de 10 de (25.639)10 102-25.639=74.361
Ejemplo : Obtener el complemento de 2 de (101100)2 26-(101100)2 = (100000)2-(101100)2=(0.1010)2
Por lo tanto tendremos que el complemento de 10 de un número decimal se puede formar dejando todos los ceros significativos sin cambios se resta el primer dígito del cero menos significativo de 10 y, entonces se restan todos los pocos dígitos menos significativos menores de 9.
El complemento de 2 puede formarse dejando todos los ceros menos significativos y el primer dígito diferente de 0 sin cambio, entonces se reemplazan los 1 por 0 y los 0 por 1 en los otros dígitos mas significativos.
b) El complemento de r-1.
Para un número positivo N en base r con una parte entera de n dígitos y una parte fraccionaria de n dígitos y una parte fraccionaria de m dígitos, el complemento de r-1 de m se define como rn-r-m-N.
Ejemplos : Obtener el complemento de 9 de (52520)10 105-100-52520=47479
Obtener el complemento de 9 de (0.3267)10 100-10-4-0.3267=0.6732
Obtener el complemento de 9 de (25.639)10 102-10-3-25.639=74.36
Obtener el complemento de 1 de (101100)2 26-20-101100=10011
Obtener el complemento de 1 de (0.0110)2 20-2-4-0.0110=
Por lo tanto deducimos que: El complemento de 9 de un número decimal se forma simplemente al restar cada dígito de 9. Y el complemento de 1 de un número binario es mas simple, ya que solo consiste en cambiar los 1 por 0 y los 0 por 1. Puesto que el complemento de r-1 es fácil de obtener, algunas veces es conveniente usarlo cuando se desea el complemento de r.
Sustracción con complemento de r.
La sustracción de 2 números positivos (M-N), ambos en base r, puede hacerse como sigue: 1.- Agréguese el minuendo m al complemento de r del sustraendo n. 2.- Verifique el resultado que se obtuvo en el paso 1 para el caso que exista un acarreo final. a) Si existe un acarreo final, descártese. b) Si no existe un acarreo final, tómese el complemento de r de número que se obtuvo en el paso 1 y colóquese un signo negativo en frente.
Ejemplo : Utilizando el complemento 10 reste 72532-03250 complemento 10 de 03250=96750 72532-96750=69282 como no existe acarreo final se utiliza el paso b).
Complemento 10 de 69282=27468 03250-27468=30718 complemento 10 de 30718=69282 resultado -69282
Utilizando el complemento 2 realice M-N con los números binarios dados. M=1010100 N=1000100
Complemento de N = 0111100
0111100
1010100
-----------
1 0010000
1011
1110
------
0101
1011
0001
------
1100
Resultado = -0011
Sustracción con complemento (r-1).
El procedimiento para esta operación es exactamente el mismo que para el complemento a r excepto por una variación llamada acarreo final.
Para la resta de M-N en base r puede calcularse tomando en cuenta los siguientes puntos: 1.- Agréguese el minuendo M al complemento de (r-1) del sustraendo N. 2.- Verifique el resultado que se obtuvo en el paso 1 para un acarreo final.
a) Si ocurre un acarreo final agréguese uno al dígito menos significativo (acarreo final desplazado). b) Si no ocurre un acarreo final tómese el complemento de (r-1) del número obtenido en le paso 1 y colóquese al frente un signo negativo.
Ejemplo : Realice el complemento de r-1 de M-N, M=72532 y N=03250 complemento 9 de N = 96749
72532 96749 -------- 1 69281
como existe un acarreo final se realiza el paso a) 69281+1=69282
Realice el complemento de r-1 de M-N, N=03250 y M=72532 complemento 9 de N = 72532
03250 27467 --------- 30717
como no existe acarreo final se realiza el paso b) complemento 9 de 30717=69282 Resultado -69282
Ejemplo : Obtener M-N para los siguiente valores, M=1010100 y N=1000100 complemento 1 de 1000100 = 0111011
1010100 0111011 ----------- 1 0001111
como existe un acarreo final se realiza el paso a)
0001111
1
----------
0010000
Suma binaria
Todas las operaciones se hacen a través de la suma binaria (operación fundamental).
Tabla de la suma
| A | B | Suma | Acarreo |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Observamos que sólo hay acarreo cuando le damos el valor de uno (1) a las dos variables.
Resta binaria
La resta consiste en una suma negada (o sea su complemento).
Ejemplo: Deseamos restar A-B. Pasos para realizarla:
- Tomamos el número A tal como está.
- El número B lo complementamos.
- Realizamos una suma de ambos valores.
- Al resultado se le agrega 1.
- El acarreo se elimina.
Representación de Números Negativos
Debido a que muchas computadoras y calculadoras digitales manejan números negativos y positivos, se necesita algún medio de representación para el signo del número (+/-). Esto se lleva a cabo en general agregando otro bit al número, denominado bit del signo.
En términos generales la convención común que se a adoptado es que un cero en el bit del signo representa un número positivo y un uno, representa un número negativo.
Ejemplo : El registro A contiene los bits 0110100, el contenido cero en el bit de mas a la izquierda (A6) es el bit del signo que representa al signo (+). Los otros seis bits son la magnitud del número, que es igual a 5210.
A6 A5 A4 A3 A2 A1 A0
0 1 1 0 1 0 0 0 110100
(+) Magnitud del numero
De este modo el número almacenado en el registro A es +52. El bit del signo se usa para indicar si un número binario almacenado es positivo o bien negativo. Para los números positivos, el resto de los bits se utilizan siempre para representar la magnitud del numero en forma binaria.
Para los números negativos, no obstante, existen tres formas posibles de representar la magnitud.
Forma de magnitud verdadera.
Forma de complemento a 1
Forma de complemento a 2
Forma de magnitud verdadera. El ejemplo visto anteriormente, contiene un bit de signo y seis bits de magnitud. Los bits de magnitud son el equivalente binario verdadero de los valores binarios que se representan.
Aunque este sistema de magnitud verdadera es directo y fácil de entender, no es de tanta utilidad como los otros dos sistemas para representar números binarios con signo. Forma de complemento a 1.
La forma de complemento a 1 de un número binario cualquiera se obtiene simplemente cambiando cada cero del número por 1 y cada uno por cero.
Ejemplo : El complemento de 1 del número 101101 es 010010 Cuando se quiere representar números negativos en forma de complemento 1 el bit de signo se convierte en 1 y la magnitud se transforma de forma binaria verdadera.
-57 = 1 111001 (forma de magnitud real)
= 1 000110 (forma de complemento a 1)
NOTA : Observe que el bit de signo no se complementa sino que se conserva en un 1 a fin de indicar un número negativo.
Forma de complemento 2.
La forma de complemento 2 de un número binario se forma simplemente tomando el complemento 1 del número y sumando 1 a la posición del bit menos significativo. Ejemplo : convertir 111001 a su forma de complemento 2.
000110
1
000111
De tal forma que -57 se escribirá como 1 000111 en su representación de complemento a 2.
Ejemplo : Tres sistemas para representar números binarios con signo se muestran a continuación. Sistema de magnitud verdadera Sistema de complemento 1 Sistema de complemento 2
+57 0 111001 0 111001 0 111001 -57 1 111001 1 000110 1 000111
NOTA :
Un número positivo en cualquier representación tiene un cero en el bit de la extrema izquierda para un (+), seguido de un número positivo. Un número negativo siempre tiene un uno en el bit de la extrema izquierda para un (-),pero los bits de magnitud se representan de una forma diferente.
En la representación de signo-magnitud, estos bits son el número positivo ; en la representación de complemento de 1, estos bits son el complemento del número binario y en la representación de complemento 2, el número esta en su forma de complemento 2.