Proporciones (Matemática)
| ||||
Las proporciones . La igualdad entre dos razones recibe el nombre de proporción. La teoría de las proporciones fue desarrollada por el gran matemático griego Eudoxio_de_Cnidos. Su obra original sobre la teoría de las proporciones no llegó hasta los tiempos actuales, pero gracias a uno de sus sucesores, Euclides de Alejandría, se pudo conocer dicha teoría, pues la recogió en su libro V de los Elementos.
Sumario
Razones y proporciones
Razón
La razón es la relación entre dos números, definida como el cociente de un número por el otro. Entonces:
La razón entre dos números a y b es la fracción ![]() y se lee a es a b. Esta razón también puede escribirse a:b.
y se lee a es a b. Esta razón también puede escribirse a:b.
Para hallar la razón entre dos números, formas el cociente entre ellos y los simplificas tanto como sea posible.
Por ejemplo, la razón entre 10 y 2 es 5, ya que 10/2=5
Proporción
Dadas dos razones ![]() y
y ![]() diremos que están en proporción si
diremos que están en proporción si ![]() =
= ![]()
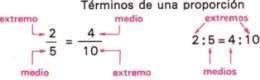
Los términos a y d se denominan extremos mientras que b y c son los medios.
En toda proporción el producto de los extremos es igual al producto de los medios
Proporcionalidad
Muchas veces en la práctica se nos presentan situaciones en las que el valor o cantidad de una magnitud depende del valor de la otra.
Por ejemplo, si un metro de tela tiene un precio de $ 10, el costo de un corte de tela depende del número de metros que tenga el largo. A mayor número de metros de tela corresponde un mayor costo.
Proporcionalidad directa
Cuando dos magnitudes están relacionadas de modo que los valores de una de ellas se obtienen multiplicando por un mismo número los valores correspondientes en la otra, se dice que son directamente proporcionales
En el ejemplo de los metros de tela, el costo del corte de tela se obtiene multiplicando la longitud del corte por el precio de un metro que es $ 10. Podemos decir entonces que el costo de una tela es directamente proporcional a la longitud del corte. El número por el que se multiplica se llama factor de proporcionalidad. En este caso es 10 ese factor.
En una proporcionalidad directa dos cantidades cualesquiera de una magnitud y sus correspondientes en la otra forman una proporción.
Proporcionalidad inversa
Existen otras formas de relaciones entre magnitudes en las que el comportamiento es diferente al de los ejemplos dados de proporcionalidad directa, en estos casos, si los valores de una aumentan, los valores correspondientes en la otra disminuyen.
Por ejemplo, si un automóvil se desplaza con una cierta velocidad y la aumenta, el tiempo que demora en llegar a su destino disminuye.
Cuando dos magnitudes están relacionadas de modo que los valores de una de ellas se obtienen multiplicando por un mismo número los recíprocos de los valores correspondientes de la otra magnitud, se dice que son inversamente proporcionales
Fuente
Libro de texto matemática sexto grado.