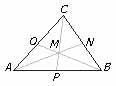
Segmentos en un triángulo plano

Segmentos en un triángulo plano son aquellos que unen el vértice de un triángulo con el lado opuesto (o su prolongación), como parte de recta o rayo, de diferentes maneras y en los diversos casos surgen con nombre propio; en ciertas clases de triángulos (isósceles, regular) y dos o más coinciden. Además, son otros segmentos trazados por puntos particulares de los lados (mediatriz).

Nomenclatura inicial

a, b, c, sus ángulos opuestos A, B, C.

semiperímetro p = (a+b+c)÷2

S = área de la región triángular

Altura

Es el segmento perpendicular trazado al lo opuesto o a la prolongación de dicho lado. Sea el ΔABC, tenemos la altura AH₁, BH₂, CH₃, denotados h_a, h_b,h_a . H_i, i=1,2,3 se llama pie de altura. Se cortan los tres en un punto llamado ortocentro.

Ortotocen- tro O de Δ acutángulo

En un Δ escaleno acutángulo, los tres pies de altura están en el lado opuesto; el ortocentro está en el interior del Δ. En un Δ escaleno obtusángulo los pies de las alturas trazadas del vértice de los ángulos agudos están en las prolongaciones de sus lados opuestos y el pie del ángulo obtuso esta en en el lado opuesto; el ortocentro está en el exterior de la figura. En un Δ escaleno rectángulo las alturas que parten de los ángulos agudos coinciden con los catetos, la altura del ángulo recto tiene su pie en la hipotenusa; su ortocentro coincide con el vértice del ángulo recto.

En un triángulo isósceles, las alturas de lados iguales tienen igual medida; si es acutángulo, el ortocentro en el interior de la figura y si obtusángulo en el exterior.

En un triángulo regular las tres alturas tienen la misma longitud, el ortocentro es punto interior de la figura.

Fórmula

h_a = 2[p(p-a)(p-b)(p-c)]÷a

h_b = 2[p(p-a)(p-b)(p-c)]÷b

h_c = 2[p(p-a)(p-b)(p-c)]÷c

Bisectriz

Es una recta que divide al ángulo interior de un triángulo en dos partes iguales. Las bisectrices concurren en punto interior, llamado incentro, que no es sino el centro de la circunferencia inscrita de radio r. En el ΔABC sean los ángulos α con vértice en A, β en B y γ en C.

El incentro I del ΔABC

Expresiones para las bisectrices

l_α = 2[bcp(p-a)]^0.5:(b+c)

l_β = 2[acp(p-b)]^0.5:(a+c)

l_γ = 2[abp(p-c)]^0.5:(b+a)

Partes de un lado con los otros lados.

Sea el triángulo ABC, la bisectriz l_α, que parte de A, corta al lado a= BC en el punto D, siendo BD = m, DC = n, los lados que convergen en A, AC = b, AB = c, entonces

m:n = b:c

Según clase triangular

• En un triángulo isósceles las bisectrices de los ángulos en la base son iguales; y la bisectriz del ángulo en el vértice ( formado por os lados iguales) coincide con la mediana, mediatriz y altura.

• En un triángulo regular las tres bisectrices son iguales ( la misma longitud). Luego la bisectriz coincide con la mediana, mediatriz y altura.

Línea media

En un triángulo se llama línea media al segmento que unen los puntos medios dee cualquier par de lados; sean L punto medio de BC; M, de AC y N, de AB.

Propiedades

Cada línea media es // al lado que no contiene los puntos medios, ademas su longitud es la mitad de la del lado paralelo.

MN // AC longitud de MN = a/2

LN // AC longitud de LN = b/2

LM // AB longitud DE LM = c/2

El ΔLMN, con vértices en los puntos medios es semejante a ΔABC y su área es 1/4 del área del triángulo contenedor.

Mediana

Se denomina mediana de un triángulo al segmento un vértice con el punto medio del lado opuesto del triángulo. Las medianas de un triángulo se intersecan en punto interior llamado baricentro ( centro de gravedad ).

Medianas de un triángulo

El baricentro corta a cada mediana en dos segmentos, uno de ellos la mitad del otro:

Fómulas

m_a = 0.5(2b^{2 + 2c2} -a²)^0.5

m_b = 0.5(2a^{2 + 2c2} -b²)^0.5

m_c = 0.5(2b^{2 + 2a2} -c²)^0.5

Propiedades

El baricentro divide a una mediana en la razón 2:1, contando desde el vértice del ángulo

La mediana es menor que la semisuma de los lados que forman el vértice del triángulo del cual parte la mediana.

En un triángulo isósceles las medianas que salen de los vértices de los ángulos en la base son iguales.

En un triángulo regular las tres medianas son iguales y su longitud m, usando la longitud a del lado común es:

M = a×(3)^0.5 :2.

Mediatriz

Se llama mediatriz de un triángulo a la recta perpendicular en el punto medio de cualesquiera de sus lados.

Propiedades

Las mediatrices de un triángulo se cortan en un mismo punto, que tiene la misma distancia a los tres vértices. El punto común se llama circuncentro y es el centro de la circunferencia circunscrita que pasa los vértices del triángulo, cuyo radio R es la distandia del circuncentro a cualquier vértice.

El área del ΔABC es S= abc:4R, siendo a, b y c los lados y r el radio de la circunfrencia circunscrita.

(27)^0.5r² ≤ S_Δ ≤ (27)^0.5R²÷4

2 r ≤ R; r radio del círculo inscrito en el triángulo y R, el del circulo circunscrito.

Ceviana

Se llama ceviana a cualquiera recta trazada del vértice de un triángulo y pasa por el lado opuesto o por la prolongación del lado opuesto. De tal modo, que la mediana, la bisectriz, la altura consideradas como rectas se pueden entender como medianas .

Teorema de Ceva

Cuando por los vértices de un ΔABC trazamos las cevianas AL, BM y CN, ellas se cortan en un único punto si y solo si

AN/NB×BL/LC×CM/MA = 1

Simediana

Se denomina simediana a la recta de un triángulo que es simétrica a la mediana respecto de la bisectriz

Propiedades

• La simediana divide el lado respectivo del triángulo en proporción directa a los cuadrados de los otros dos lados.
• La simediana es el lugar geométrico de todos los puntos para los cuales las distancias a los lados adyacentes son directamente proporcionales a las longitudes de tales lados.
• El punto común de las tres simedianas coincide con el punto de Lemoine, este es el punto cuyas distancias a los tres lados son proporcionales a estos

Fórmula

s_a = bc[2(b²+c²) - a²]^0.5 ÷ (b²+c²)

Fuentes

• Elementos de Geometría de G. M. Bruño.
• A. V. Pogorélov: Geometría elemental, ditorial Mir, Moscú- 1974
• S. B. Gashkov: Desigualdades geométricas, Editorial URSS, Moscú, 2015
• https://www.google.com/search?q=Segmentos+en+un+tri%C3%A1ngulo+plano&tbm=isch&source=univ&client=firefox-b-d&sa=X&ved=2ahUKEwiz26aTu4rlAhWSm1kKHUCeBf4QsAR6BAgAEAE&biw=1360&bih=590#imgrc=kEcTzmgcoYhLHM: