Bifurcación de Hopf
Bifurcación de Hopf
En matemática, una bifurcación de Hopf (también llamada bifurcación de Poincaré-Hopf-Andronov o bifurcación de Andronov-Hopf) se refiere a la desaparición o aparición local de un equilibrio de una solución periódica (oscilación auto-excitado...un ciclo límite) de ecuaciones diferenciales ordinarias que describen un sistema dinámico con cual ese equilibrio (valores críticos) cambia estabilidad cuando, y solo cuando, el parámetro se varia de valor por la “derecha” o la “izquierda”, o matemáticamente, a través de un par de valores propios (eigenvalores) puramente imaginarios que cruzan el eje imaginario en el plano complejo hacia la parte derecha (la parte real).[1]
La bifurcación puede ser supercrítico o subcrítico, siendo estable o inestable (dentro de una variedad, "manifold" en ingles, invariante de dos dimensiones) ciclo límite. El ciclo límite es un conjunto que atrae con cual orbitos y trayectorias convergen y cual las trayectorias son periódicas.[2] Una variedad es el objeto geométrico que generaliza la noción intuitiva de curva y de superficie a cualquier dimensión y sobre cuerpos diversos.
Bifurcación de Hopf aparecen en sistemas de ecuaciones diferenciales con 2 dimensiones mínimo, y como se ha dicho, cuando un punto cambia su estabilidad y aparece un ciclo límite. Es decir, una bifurcación de Hopf genera un ciclo límite de un punto fijo.
Sumario
Historia
En general, el nombre "bifurcación" (abreviado “bif'n”) fue introducido por primera vez por Henri Poincaré en 1885 en el primer documento de matemáticas que muestran un comportamiento de ese tipo[3]. Poincaré también nombró varios tipos de puntos estacionarios y los clasificó[4].
La bifurcación de Hopf también se conoce como bifurcación de Poincaré-Hopf-Andronov (por Henri Poincaré, Eberhard Hopf, y Aleksandr Andronov). Cuidado en no confundir a Heinz Hopf (1894-1971) que fue un matemático alemán en los campos de la topología y la geometría con Eberhard Hopf.
Eberhard Frederich Ferdinand Hopf (1902, Salzburgo, Austria-Hungría - 1983, Bloomington, Indiana) fue un matemático y astrónomo, uno de los padres fundadores de la teoría ergódica y un pionero de la teoría de la bifurcación que también hizo contribuciones significativas a los temas de ecuaciones diferenciales parciales y ecuaciones integrales, dinámica de fluidos, y la geometría diferencial. El principio del máximo Hopf es un resultado temprano de su (1927), que es una de las técnicas más importantes en la teoría de ecuaciones diferenciales parciales elípticas.
Aleksandr Aleksandrovich Andronov (ruso: Александр Александрович Андронов; 1901, Moscú - 1952, Gorki) fue un físico soviético y miembro de la Academia Soviética de Ciencias (1946). El cráter Andronov en la Luna lleva su nombre. Se trabajó intensamente en la teoría de la estabilidad de los sistemas dinámicos, la introducción (con Lev Pontryagin) la noción de estabilidad estructural. En ese contexto, también contribuyó a la teoría matemática de la auto-oscilación (un término que él nombro).
Definición
La definición en palabras de una bifurcación de Hopf es la aparición o la desaparición de una órbita periódica a través de un cambio local en las propiedades de estabilidad (parámetro) de un punto de equilibrio. Es decir, la bifurcación de Hopf es un punto crítico en el que la estabilidad de un sistema cambia y surge una solución periódica[5]. Tabor (1989), lo dice con otras palabras: es la bifurcación de un punto fijo a un ciclo límite[6]. Weisstein (2004), mas o menos lo repite: un bifurcación (cambio) de un punto fijo a un ciclo límite.
Definición: Condiciones de aparición de ciclos límite de un sistema dinámico.
- dx/dt = f(x, C) con x ∈ R y C ∈ R y con f(xo, Co) = 0
Aparece un ciclo límite cuando un par de eigenvalores complejos del jacobiano
- J(C) = Dxf(xo(C), C) que cruzan el eje imaginario en el plano complejo,
y que no satisface la condición de transversalidad,
- es decir, donde, d/dc [R {(λ(C)}] = 0, no es valido (no es cero).
siendo Co el valor para el que J(Co) tiene sólo un par de eigenvalores imaginaros puros.[7]
Teorema de Hopf
El teorema de la bifurcación de Hopf usa un par de números complejos (que son puntos conjugados) como condición en la que se produce el fenómeno de bifurcación de Hopf.
Teorema: Sea Jo el Jacobiano de un sistema dinámico evaluado en un punto de equilibrio, y que se suponga que todos los valores propios (eigenvalores) de Jo tienen partes reales que son negativas, excepto un par conjugado no-cero puramente imaginario, entonces una bifurcación de Hopf surge cuando este par de eigenvlaores cruzan el eje imaginario por causa de variación del parámetro.
Básicamente, la teorema demuestra que la amplitud y frecuencia de una solución periódica de un sistema dinámico puede ser aproximadamente calculado cuando se varía un parámetro importante.[8]
Forma
La forma normal de una bifurcación es un sistema dinámico simple que es equivalente a todos los sistemas que muestran esta bifurcación.[9]
La forma normal para la bifurcación de Hopf es:
- dx/dt = x((C + i) + a|x|2, donde x, a son complejo con C siendo el parámetro.
Si se escribe con a = L + ib, entonces L es el primer coeficiente de Lyapunov.
si L es negativo, entonces hay un ciclo límite estable y la bifurcación se le llama supercrítico. si L es positivo, entonces hay un ciclo límite inestable y la bifurcación se le llama subcrítico.
Coeficiente de Lyapunov
La bifurcación de Hopf es subcrítico o supercrítico dependiendo en la señal del primer coeficiente de Lyapunov.
Un ciclo límite es orbital estable si el primer coeficiente de Lyapunov es negativo y la bifurcación es supercrítico. De lo contrario, es inestable y la bifurcación es subcrítico.
Un ciclo límite aparece mientras que el enfoque cambia estabilidad. La dirección del ciclo se determina por el primer coeficiente de Lyapunov:
- 1.) supercritical (suave, no catastrófico) si el primer coeficiente de Lyapunov es negativo
- 2.) subcritical (duro, catastrófico) si el primer coeficiente de Lyapunov es positivo[10]
Eigenvalor
La importancia del valor propio (o eigenvalor), el Jacobiano (matriz jacobiana), y los números complejos se puede ver en el ejemplo de la teorema de Hopf que dice que en el plano imaginario las bifurcaciones ocurren cuando los dos eigenvalores cruzan la parte derecha del plano (la parte real que es positivo).
Ejemplo 1
Un ejemplo de dimensión 2 (subcrítico), las ecuaciones diferenciales:
- dx/dt = A –CX – X + X2Y;
- dy/dt = CX – X2Y
donde C es el parámetro que se varia para observar un cambio cualitativo (en este ejemplo sera un bifurcación de Hopf) en el sistema dinámico (que en este caso es una reacción química).
Los puntos de equilibrios del sistema de las ecuaciones diferenciales son calculado resolviendo las ecuaciones:
- a – cx – x + x2y = 0;
- cx - x2y = 0
sumando las dos ecuaciones resulta en x = a
Así que el único punto de equilibrio es (a, c/a)
Para determinar la estabilidad del sistema se usa el Jacobiano:
D[f(x,y)] = | D(1,1) = -c-1+2xy; D(1,2)= x2; D(2,1)= c-2xy; D(2,2) = -x2 |
D[f(a, c/a)] = | D(1,1) = c-1; D(1,2) = a2; D(2,1)= -c; D(2,2) = -a2 |
- Traza (D[f(a, c/a)]) = - a2 + c – 1; estable espiral si la traza es negativo, sino inestable
- Det (D[f(a, c/a)]) = a2
Como el determinante siempre es positivo, nunca cero, el punto de equilibrio nunca es silla-nodo[11].
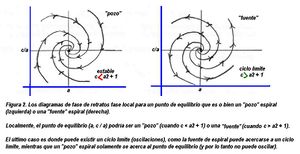
- cuando a = 2, c < a2 + 1, c < 5 estable, asi que no hay ciclos límite;
- cuando a = 2, c > 5 si hay ciclos límite porque el espiral se aleja de cero (Figura 2).
Así que el punto c = a2 + 1 es un bifurcación de Hopf y es subcrítico.
Para demostrar que existe una bifurcación de Hopf use la teorema de la bifurcación de Hopf (que los valores propios son puro imaginarios y no nulo). En este ejemplo también es posible en la presencia de difusión tener inestabilidad de Turing.
Se le recuerda que el ciclo límite es de orbital estable si el primer coeficiente de Lyapunov es negativo y la bifurcación es supercrítico. De lo contrario, es inestable y la bifurcación es subcrítico.
Este ejemplo demuestra el “Brusselator”, que es un tipo de reacción-difusión que es autocatalítica (un proceso mediante el cual un compuesto químico induce y controla una reacción química sobre sí mismo). El Brusselator es una reacción química que es oscilante y no lineal (por ser autocatalítica) y fue polémico en los 1900 y pico entre químicos. Fue propuesto por Ilya Prigogine en la Universidad Libre de Bruselas. El nombre es un acrónimo de Brussels (‘Bruselas’) y oscillator (‘oscilador’). La "más pequeña reacción química con bifurcación de Hopf" fue encontrado en 1995 en Berlín, Alemania[12].
Otros ejemplos
Bifurcación de Hopf se produce también en ecuaciones diferenciales ordinarias con infinitamente dimensiones generadas por las ecuaciones diferenciales parciales y de retardo, a la que se aplica el Centro Múltiple Teorema, que es una manera de simplificar los sistemas dinámicos mediante la reducción de la dimensión del sistema. Un análogo de la bifurcación de Hopf, llamada bifurcación de Neimark-Sacker, ocurre en los sistemas dinámicos generados por mapas iterados cuando el punto fijo crítico tiene un par de eingenvalores e ± iθ.
La bifurcación de Bautin es una bifurcación de un equilibrio en una familia de dos parámetros de ecuaciones diferenciales ordinarias autónomas a la que el equilibrio crítico tiene un par de eigenvalores puramente imaginarios y el primer coeficiente de Lyapunov para la bifurcación de Hopf se desaparece. Este fenómeno se llama bifurcación generalizada de Hopf.
Véase también
- Bifurcaciones de ecuaciones diferenciales
- Bifurcación silla-nodo
- Bifurcación transcrıtica
- Bifurcación tridente
Referencias
- ↑ Yuri A. Kuznetsov (2006) Andronov-Hopf bifurcation. Scholarpedia, 1(10):1858
- ↑ Weisstein, Eric W. "Limit Cycle." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/LimitCycle.html
- ↑ Henri Poincaré. "L'Équilibre d'une masse fluide animée d'un mouvement de rotation". Acta Mathematica, vol.7, pp. 259-380, Sept 1885.
- ↑ History of dynamical systems http://www.scholarpedia.org/article/History_of_dynamical_systems
- ↑ Hopf Bifurcations. MIT. http://ocw.mit.edu/courses/mathematics/18-385j-nonlinear-dynamics-and-chaos-fall-2004/lecture-notes/hopfbif.pdf
- ↑ Weisstein, Eric W. "Hopf Bifurcation." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/HopfBifurcation.html
- ↑ Jorge L Moiola, Guanrong Chen. World Scientific, Apr 9, 1996 Hopf Bifurcation Analysis: A Frequency Domain Approach https://books.google.com/books/about/Hopf_Bifurcation_Analysis.html?id=k_fsCgAAQBAJ
- ↑ Preface page vii Moiola, Chen. '96 Hopf Bifurcation Analysis https://books.google.com/books/about/Hopf_Bifurcation_Analysis.html?id=k_fsCgAAQBAJ
- ↑ Guckenheimer, John; Holmes, Philip (1983), Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, Springer, Section 3.3, ISBN 0-387-90819-6.
- ↑ Bifurcation Phenomena Lecture 2: One-parameter bifurcations of planar ODEs Yuri A. Kuznetsov http://www.staff.science.uu.nl/~kouzn101/cm/L2.pdf
- ↑ Dynamics of the Brusselator, Shaun Ault Erik Holmgreen, 3/16/2003 http://www-dimat.unipv.it/~boffi/teaching/download/Brusselator.pdf
- ↑ Wilhelm, T.; Heinrich, R. (1995). "Smallest chemical reaction system with Hopf bifurcation". Journal of Mathematical Chemistry 17 (1): 1–14. doi:10.1007/BF01165134.